Research: Quantum Systems Theory
Research areas
The Theory Group is active in several research areas. Its activity is focused on the development of theoretical tools based on geometric and topological methods to explain phenomena in various contexts. The developed methodologies have been mainly applied to three research fields: the characterisation of phase-transition phenomena in classical Hamiltonian systems, the study of dynamical phenomenology of classical and quantum systems, and the characterisation of entanglement and quantum correlation properties, in quantum multipartite states. In the following, we list our main objectives in the macro-areas of investigation: Quantum Science Theory, Statistical Mechanics and Dynamical Systems. Despite the strong differences among them, the studies in the three macro areas share similar mathematical methods.
Quantum Science Theory
Entanglement has an important role in quantum science theory and the development of quantum technologies. It is a valuable resource in quantum cryptography, in quantum computation, in teleportation and in quantum metrology. Nevertheless, entanglement measure and characterisation remain elusive and the problem of its quantification in the case of a general system, is still open. In the last decades, several approaches have been developed to quantify the entanglement in the variety of quantum states. Rigorous achievements in the explicit quantification of entanglement, are limited to bipartite systems case. The entropy of entanglement is uniquely accepted as a measure of entanglement for pure states of bipartite systems. Entanglement of formation, entanglement distillation and relative entropy of entanglement are largely acknowledged as faithful measures for bipartite mixed systems. An extensive literature is devoted to the study of entanglement in multipartite systems. Up to now, different approaches have been proposed including, e.g. in the case of pure states, the study of the equivalence classes in the set of multipartite entangled states, whereas, the study of entanglement in mixed multipartite states has been addressed, e.g., with a Schmidt measure or with a generalisation of concurrence. In the last years, have been proposed entanglement estimation-oriented approaches and derived from a statistical distance concept, such as, for instance, the quantum Fisher information. In [1] we have put forward a new entanglement measure able to quantify by a direct calculation, the degree of entanglement of a general multi-qudit hybrid pure state. Such entanglement measure, named entanglement distance (ED), derives from a minimum distance principle.

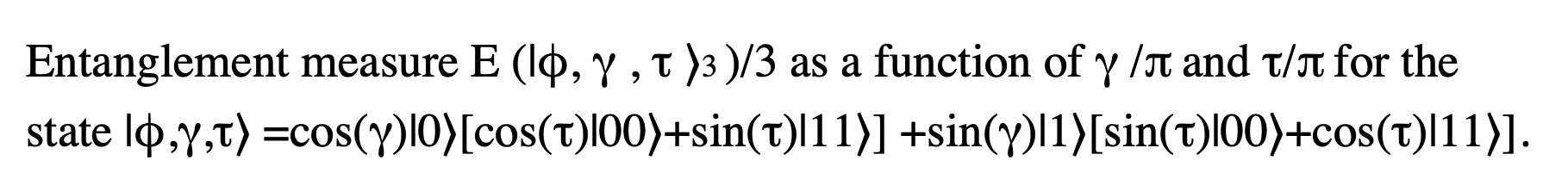
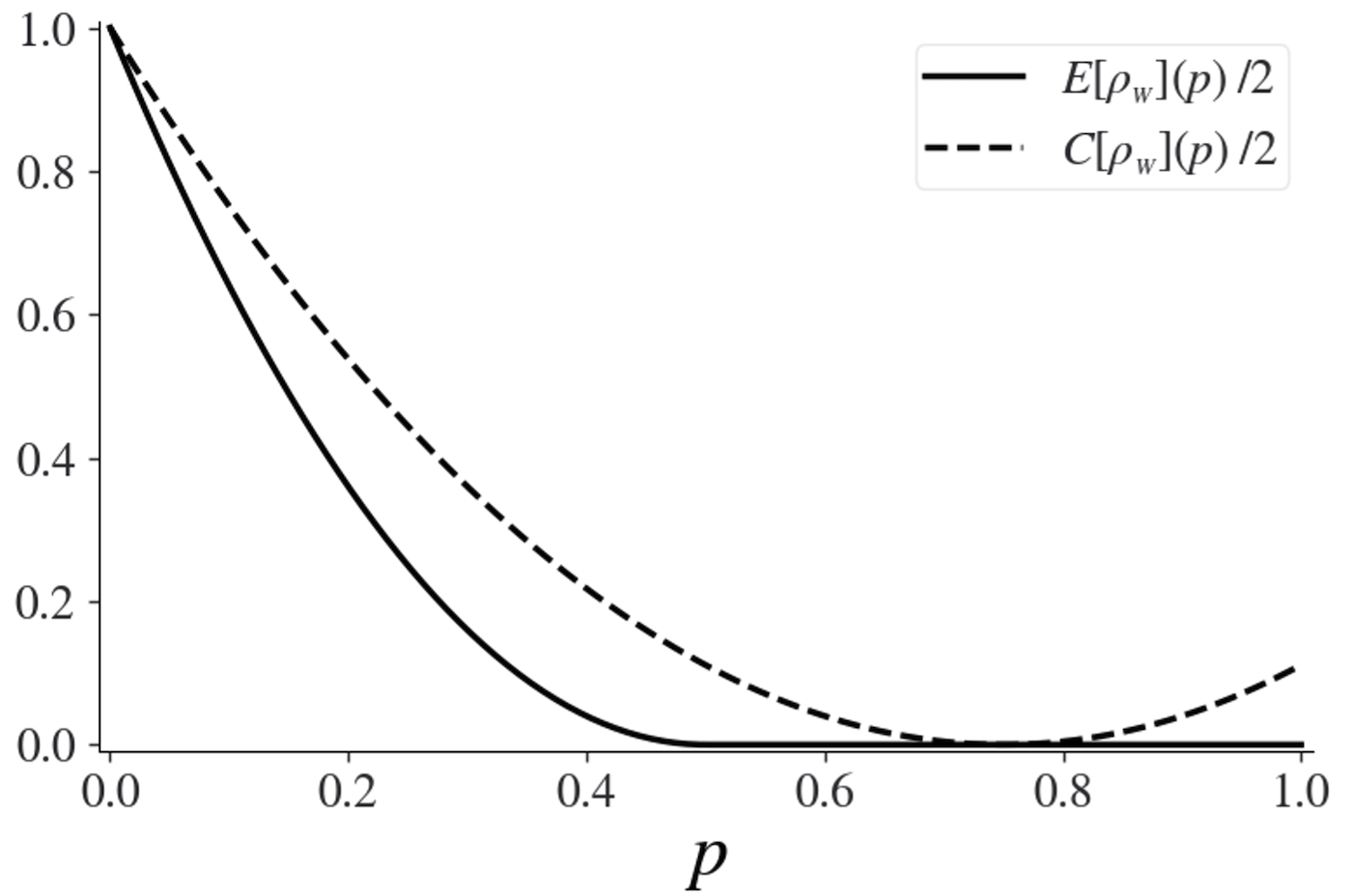

A pure state is entangled if manifests any quantum correlation between its components and vice versa. In fact, entanglement and correlation are rather equivalent in the case of pure states. On the contrary, in the case of mixed states, one can observe states that manifest correlations detached from entanglement. In the [2] we have proposed a new measure of quantum correlation, and a related entanglement measure for mixed states, derived from the first through a regularisation process. Such entanglement measure derives from a minimum distance principle and, for this reason, we name it entanglement distance.
Related papers:
[1] D. Cocchiarella, S. Scali, S. Ribisi, B. Nardi, G. Bel-Hadj-Aissa, and R. Franzosi, “Entanglement distance for arbitrary M-qudit hybrid systems”, Phys. Rev. A 101, 042129 (2020).
[2] A. Vesperini, G. Bel-Hadj-Aissa, and R. Franzosi, Entanglement and quantum correlation measures for quantum multipartite mixed states, Scientific Reports 13 2852 (2023).
[3] A. Nourmandipour, A. Vafafard, A. Mortezapour and R. Franzosi, “Entanglement protection of classically driven qubits in a lossy cavity”, Scientific Reports (2021) 11:16259.
[4] A. Vafafard, A. Nourmandipour, and R. Franzosi, Multipartite stationary entanglement generation in the presence of dipole-dipole interaction in an optical cavity, Phys Rev A 105, 052439 (2022).
[5] S. Scali and R. Franzosi, “Entanglement estimation in non-optimal qubit states”, Annal of Physics 411 (2019) 167995.
Statistical Mechanics
Phase transitions phenomena are ubiquitous in nature and are phenomena that take place at very different scales in space and in energy. From the theoretical point of view, understanding their origin, and being able to classifying them, is of central interest. In spite of a huge literature on this topic, a general theory is still lacking. In the Landau’s phenomenological theory, phase transitions are related to the mechanism of spontaneous symmetry breaking. However, Landau’s theory is not all-encompassing. Many systems do not fit in this theory, for instance, systems undergoing a phase transition without spontaneous symmetry breaking, or without an order parameter. Notable examples are: Kosterlitz–Thouless transitions after Mermin–Wagner theorem, systems with local gauge symmetries after Elitzur’s theorem, liquid–gas transitions, transitions in supercooled glasses and liquids, transitions in amorphous and disordered systems, folding transitions in homopolymers and proteins. In the mathematical description of phase transitions, the loss of analyticity of thermodynamic observables is explained by resorting to the thermodynamic limit (limit of an infinite number of particles). This limit is considered, for instance in the Yang–Lee theory and in the Dobrushin–Lanford–Ruelle theory. As a matter of fact, contemporary research on nanoscopic and mesoscopic systems, on the biophysics of polymers, on Bose–Einstein condensation, Dicke superradiance in microlaser, superconducting transitions in small metallic objects, pertain to transition phenomena in systems of finite number of particles.
Within all the hitherto developed theoretical frameworks, for instance theory of renormalisation group and critical phenomena, it is assumed that the primitive object at the grounds of a theory is the statistical measure; the gran-canonical measure in the Yang–Lee theory, the canonical measure in the Dobrushin–Lanford–Ruelle theory, and the microcanonical measure in more recent approaches. However, several results suggest that a phase transition depends on some measure-independent properties, as the spatial dimension, the dimensionality of the order parameter, the range of its interactions, the symmetry group of the Hamiltonian. This suggest that the information might be encoded already at a more fundamental level, completely determined by the internal interactions of a system, namely by the potential function. A complementary approach to the existing theories is a well-motivated and timely purpose.
We have put forward a new starting point for a line of thought based on a variety of results which hitherto did not appear to fit in a coherent theoretical framework. In fact, the investigation of the Hamiltonian dynamical counterpart of phase transitions, combined with the study of the Riemannian geometrisation of dynamics, has led to a preliminary formulation of a differential-topological theory of phase transitions: in correspondence of a phase transition there are peculiar geometrical changes of the mechanical manifolds that stem from changes of their topology. These findings, together with two theorems [6,7], have suggested that a topological theory of phase transitions can be formulated to go beyond the limits of the existing theories. The new theory applies to phase transitions in small N systems (that is, at nanoscopic and mesoscopic scales), and in the absence of symmetry-breaking. However, the preliminary version of the theory was incomplete and still falsifiable by counterexamples. Furthermore, in a recent work [8] we have provided a relevant leap forward leading to an accomplished development of the topological theory of phase transitions paving the way to further developments and applications of the theory that can be no longer hampered.
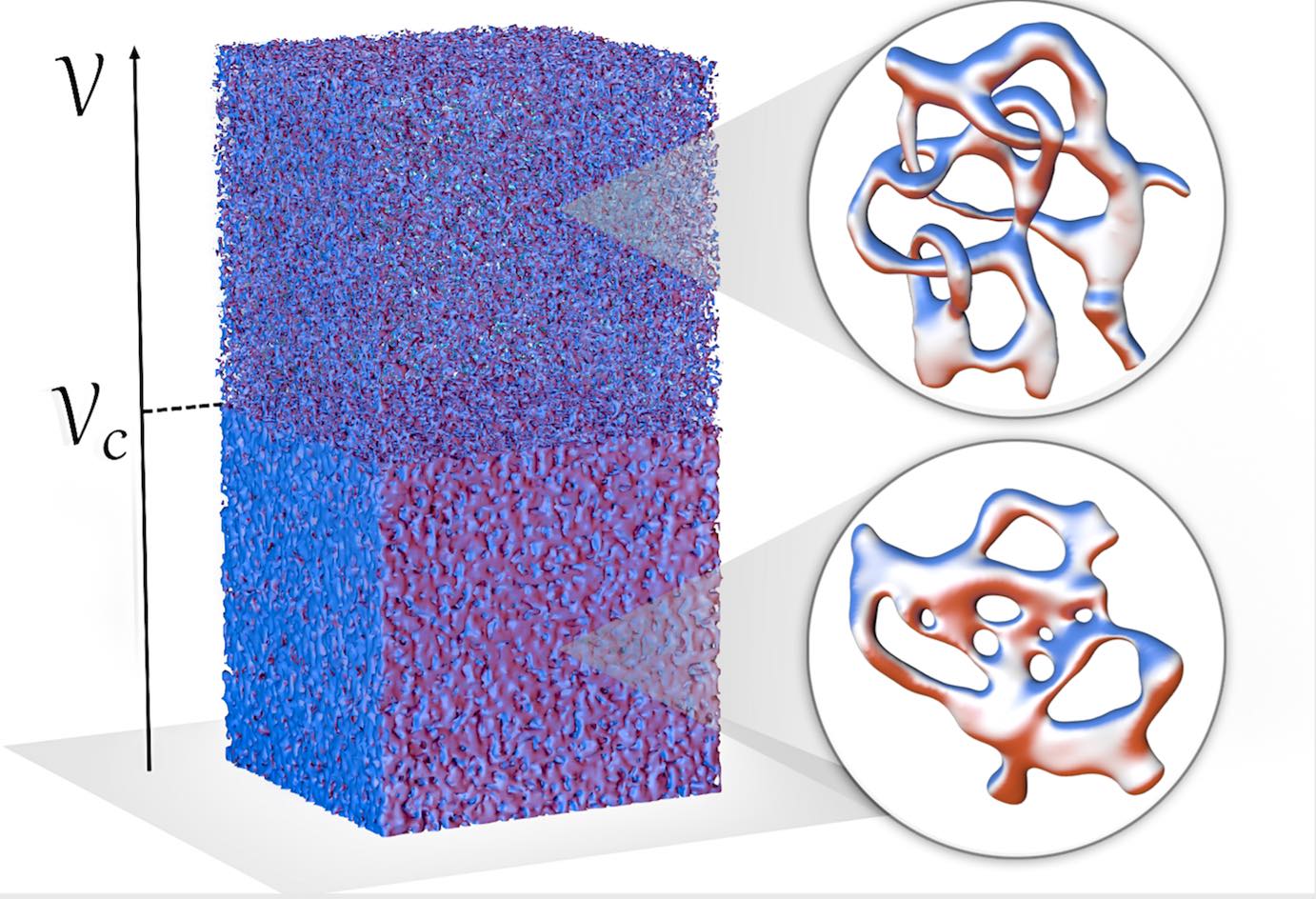
 Selected related papers:
Selected related papers:
[6] R. Franzosi, M. Pettini and L. Spinelli, “Topology and Phase Transitions I. Preliminary Results”, Nuclear Physics B 782 (2007) 189-218
[7] R. Franzosi and M. Pettini, “Topology and Phase Transitions II. Entropy and Topology”, Nuclear Physics B 782 (2007) 219-240
[8] M. Gori, R. Franzosi, G. Pettini and M. Pettini, Topological Theory of Phase Transitions, J. Phys. A: Math. Theor. 55 (2022) 375002.
[9] A. Vafafard, A. Nourmandipour, and R. Franzosi, Multipartite stationary entanglement generation in the presence of dipole-dipole interaction in an optical cavity, Phys Rev A 105, 052439 (2022).
Dynamical Systems
A suitable geometric approach to the study of the dynamics of classical, semi-classical, and quantum systems, can open the door to information, also by numeric simulations, otherwise of difficult access. For instance, for an isolated many-body classical system, the ergodicity makes equivalent thermodynamics and dynamics. Thus, in these cases, one can measure thermodynamic quantities, like temperature and specific heat, as temporal averages of suitable functions along almost each trajectory of a given system, or, equivalently, as an integral over its phase space. The opportunity to pass from the dynamics to the microcanonical-thermodynamics and vice versa, gives the possibility to choose the smarter way to measure a given quantity [16].
Selected related papers:
[13] R. Franzosi and V. Penna, “Chaotic behavior, collective modes and self-trapping in the dynamics of three coupled Bose-Einstein condensates”, Phys. Rev. E, 67, 046227 (2003).
[14] P. Buonsante, R. Franzosi, and V. Penna, “Dynamical Instability in a Trimeric Chain of Interacting Bose-Einstein Condensates”, Phys. Rev. Lett., 90, 050404 (2003).
[15] R. Livi, R. Franzosi and G.-L. Oppo, “Selflocalization of Bose-Einstein condensates in optical lattices via boundary dissipation”, Phys. Rev. Lett. 97, 060401 (2006).
[16] R. Franzosi, “Microcanonical entropy and dynamical measure of temperature for systems with two first integrals”, J. Stat. Phys. (2011) 143: 824–830.
[17] R. Franzosi, R. Livi, G.-L. Oppo and A. Politi “Discrete Breathers in Bose-Einstein Condensates”, Nonlinearity 24 (2011) R89-R122.
[18] S. Iubini, R. Franzosi, R. Livi, G.-L. Oppo and A. Politi, “Discrete breathers and negative- temperature states”, New J. Phys. 15 (2013) 023032.
[19] S. Iubini, R. Franzosi, R. Livi, G.-L. Oppo and A. Politi, “Discrete breathers and negative- temperature states”, New J. Phys. 15 (2013) 023032.
[20] R. Franzosi, D. Felice, S. Mancini, M. Pettini, “A geometric entropy detecting the Erdös-Rényi phase transition”, EPL, 111 (2015) 20001.
[21] P. Buonsante, R. Franzosi and A. Smerzi, “On the dispute between Boltzmann and Gibbs entropy”, Annals of Physics 375 (2016) 414–434.
[22] E. Faraji, R. Franzosi, S. Mancini and M. Pettini, “Transition between random and periodic electron currents on a DNA chain”, Int. J. Mol. Sci. 2021, 22, 7361.
[23] E. Faraji, R. Franzosi, S. Mancini and M. Pettini, “Transition between random and periodic electron currents on a DNA chain”, Int. J. Mol. Sci. 2021, 22, 7361.
